CertifyTech

FILTER TRANSFER FUNCTIONS

An infinite number of filter transfer functions exist. A handful are commonly used as a starting point due to certain characteristics. The table following the plots lists properties of the filter types shown below. Not given - due to complex numerical methods required - are the Cauer (Elliptical) filters that exhibit equiripple characteristic in both the passband and the stopband.

Phase information may be gleaned from the transfer functions by separating them in to real and imaginary parts and then using the relationship:

Phase: q = tan^-1 (Im / Re)

Group delay is defined as the negative of the first derivative of the phase with respect to frequency, or

Group Delay: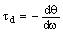

Filter Responses

Type	Properties	Transfer Function (Lowpass)
Butterworth	Maximally flat near the center of the band. Smooth transition from passband to stopband. Moderate out-of-band rejection. Low group delay variation near center of band. Moderate group delay variation near band edges.
Chebychev	Equiripple in passband. Abrupt transition from passband to stopband. High out-of-band rejection. Rippled group delay near center of band. Large group delay variation near band edges.
Bessel	Rounded amplitude in passband. Gradual transition from passband to stopband. Low out-of-band rejection. Very flat group delay near center of band. Flat group delay variation near band edges^[1].	Note: B_N, P_N, and bo_N must be placed in a loop from 0 through N.
Ideal	Flat in the passband. Step function transition from passband to stopband. Infinite out-of-band rejection. Zero group delay everywhere.	(Heaviside step function)

[1] Filters with a large BW will exhibit sloped group delay across the band. This usually is not a problem since group delay deviation tends to be specified for variation in some subsection of the band.

Band Translations