RADAR  EQUATION

RADAR CROSS SECTION  

Radar cross section is the measure of a target's ability to reflect radar signals in the direction of the radar receiver, i.e. it is a measure of the ratio of backscatter power per steradian (unit solid angle) in the direction of the radar (from the target) to the power density that is intercepted by the target.

The RCS of a target can be viewed as a comparison of the strength of the reflected signal from a target to the reflected signal from a perfectly smooth sphere of cross sectional area of 1 m² as shown in Figure 1.

The conceptual definition of RCS includes the fact that not all of the radiated energy falls on the target. A target's RCS () is most easily visualized as the product of three factors:

= Projected cross section x Reflectivity x Directivity .

RCS() is used in the Two-Way Radar Equation Section for an equation representing power reradiated from the target.

Reflectivity: The percent of intercepted power reradiated (scattered) by the target.

Directivity: The ratio of the power scattered back in the radar's direction to the power that would have been backscattered had the scattering been uniform in all directions (i.e. isotropically).

Figure 2 shows that RCS does not equal geometric area. For a sphere, the RCS, = r², where r is the radius of the sphere.

The RCS of a sphere is independent of frequency if operating at sufficiently high frequencies where <<Range, and << radius (r). Experimentally, radar return reflected from a target is compared to the radar return reflected from a sphere which has a frontal or projected area of one square meter (i.e. diameter of about 44 in). Using the spherical shape aids in field or laboratory measurements since orientation or positioning of the sphere will not affect radar reflection intensity measurements as a flat plate would. If calibrated, other sources (clyinder, flat plate, or corner reflector, etc.) could be used for comparitive measurements.

To reduce drag during tests, towed spheres of 6", 14" or 22" diameter may be used instead of the larger 44" sphere, and the reference size is 0.018, 0.099 or 0.245 m² respectively instead of 1 m². When smaller sized spheres are used for tests you may be operating at or near where ~ radius. If the results are then scaled to a 1 m² reference, there may be some perturbations due to creeping waves. See the discussion at the end of this section for further details. RCS can also be expressed in decibels referenced to a square meter (dBsm) which equals 10 log (RCS in m²).

For a flat plate which is frequency dependent , the RCS, = 4a²/², where a is the area of the plate.

Figure 3 depicts backscatter from common shapes.

A sphere reflects equally in all directions.

A flat plate that is perpendicular to the radar line-of-sight reflects directly back at the radar.

A tilted plate reflects away from the radar.

A corner reflects directly back to the radar somewhat like a flat plate.
In Figure 4, RCS patterns are shown as objects are rotated about their vertical axes (the arrows indicate the direction of the radar reflections).

The sphere is essentially the same in all directions.

The flat plate has almost no RCS except when aligned directly toward the radar.

The corner reflector has an RCS almost as high as the flat plate but over a wider angle.

Targets such as ships and aircraft often have many effective corners. Corners are sometimes used as calibration targets or as decoys, i.e. corner reflectors.

An aircraft target is very complex. It has a great many reflecting elements and shapes. The RCS of real aircraft must be measured. It varies significantly depending upon the direction of the illuminating radar.

Figure 5 shows a typical RCS plot of a jet aircraft. The plot is an azimuth cut made at zero degrees elevation (on the aircraft horizon). Within the normal radar range of 3-18 GHz, the radar return of an aircraft in a given direction will vary by a few dB as frequency and polarization vary (the RCS may change by a factor of 2-5). It does not vary as much as the flat plate.

As shown in Figure 5, the RCS is highest at the aircraft beam due to the large physical area observed by the radar and perpendicular aspect (increasing reflectivity). The next highest RCS area is the nose/tail area, largely because of reflections off the engines or propellers. Most self-protection jammers cover a field of view of +/- 60 degrees about the aircraft nose and tail, thus the high RCS on the beam does not have coverage. Beam coverage is frequently not provided due to inadequate power available to cover all aircraft quadrants, and the side of an aircraft is theoretically exposed to a threat 30% of the time over the average of all scenarios.

Typical radar cross sections are as follows: Missile 0.5 sq m; Tactical Jet 5 to 100 sq m; Bomber 10 to 1000 sq m; and ships 3,000 to 1,000,000 sq m.

Again, Figure 5 shows that these values can vary dramatically. The strongest return depicted in the example is 100 m² in the beam, and the weakest is slightly more than 1 m² in the 135/225 positions. These RCS values can be very misleading because other factors may affect the results. For example, phase differences, polarization, surface imperfections, and material type all greatly affect the results. In the above typical bomber example, the measured RCS may be much greater than 1000 square meters in certain circumstances (90, 270).

SIGNIFICANCE OF THE REDUCTION OF RCS

If each of the range or power equations that have an RCS () term is evaluated for the significance of decreasing RCS, Figure 6 results. Therefore, an RCS reduction can increase aircraft survivability.

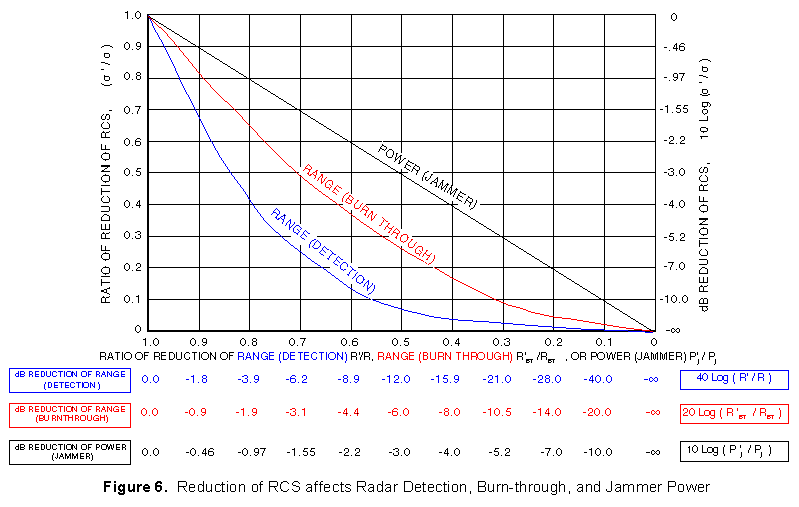The equations used in Figure 6 are as follows:

Range (radar detection): From the two-way range equation:

Therefore, R⁴ is proportional to or ^1/4 is proportional to R

Range (radar burn-through): The crossover equation has:

Therefore, R_BT² is proportional to or ^1/2 is proportional to R_BT

Power (jammer): Equating the received signal return (P_r) in the two way range equation to the received jammer signal (P_r) in the one way range equation, the following relationship results:

Therefore, P_j is proportional to or is proportional to P_j
Note: jammer transmission line loss is combined with the jammer antenna gain to obtain G_t.

Example of Effects of RCS Reduction - If the RCS of an aircraft is reduced to 0.7 (70%) of its original value, then
(1) the jammer power required to achieve the same effectiveness would be 0.7 (70%) of the original value (or -1.55 dB). Likewise,
(2) If Jammer power is held constant, then burnthrough range is 0.84 (84%) of its original value (-1.55 dB), and
(3) the detection range of the radar for the smaller RCS target (jamming not considered) is 0.91 (91%) of its original value (-1.55 dB).

OPTICAL / MIE / RAYLEIGH REGIONS

Figure 7 shows the different regions applicable for computing the RCS of a sphere.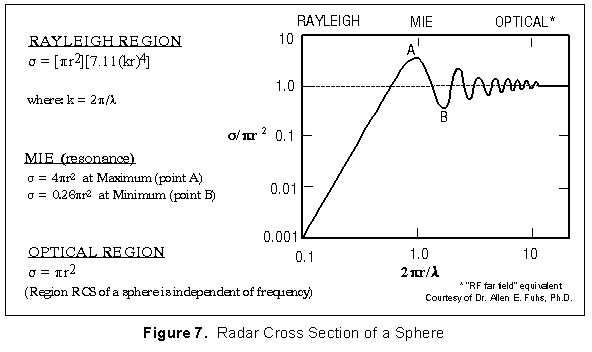

The optical region ("far field" counterpart) rules apply when 2r/ > 10. In this region, the RCS of a sphere is independent of frequency. Here, the RCS of a sphere, = r². The RCS equation breaks down primarily due to creeping waves in the area where ~ 2r. This area is known as the Mie or resonance region. If we were using a 6" diameter sphere, this frequency would be 0.6 GHz. (Any frequency ten times higher, or above 6 GHz, would give expected results). The largest positive perturbation (point A) occurs at exactly 0.6 GHz where the RCS would be 4 times higher than the RCS computed using the optical region formula. Just slightly above 0.6 GHz a minimum occurs (point B) and the actual RCS would be 0.26 times the value calculated by using the optical region formula. If we used a one meter diameter sphere, the perturbations would occur at 95 MHz, so any frequency above 950 MHz (~1 GHz) would give predicted results.

CREEPING WAVES

The initial RCS assumptions presume that we are operating in the optical region (<<Range and <<radius). There is a region where specular reflected (mirrored) waves combine with backscattered creeping waves both constructively and destructively as shown in Figure 8. Creeping waves are tangential to a smooth surface and follow the "shadow" region of the body. They occur when the circumference of the sphere ~ and typically add about 1 m² to the RCS at certain frequencies.

As also shown in Figure 1, an aircraft may not be detected because it is below the radar line which is tangent to the earths surface.

Some rules of thumb are:

Range (to horizon):

Range (beyond horizon / over earth curvature):

In obtaining the radar horizon equations, it is common practice to assume a value for the Earth's radius that is 4/3 times the actual radius. This is done to account for the effect of the atmosphere on radar propagation. For a true line of sight, such as used for optical search and rescue, the constant in the equations changes from 1.23 to 1.06 (see later equations which round this to 1.05 for ease of computing).

A nomograph for determining maximum target range is depicted in Figure 2. Although an aircraft is shown to the left, it could just as well be a ship, with radars on a mast of height "h". Any target of height (or altitude) "H" is depicted on the right side.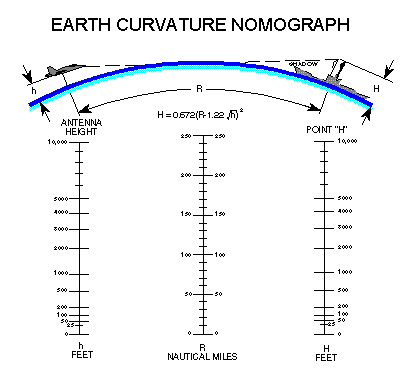

This data was expanded to consider the maximum range one aircraft can detect another aircraft in Figure 3.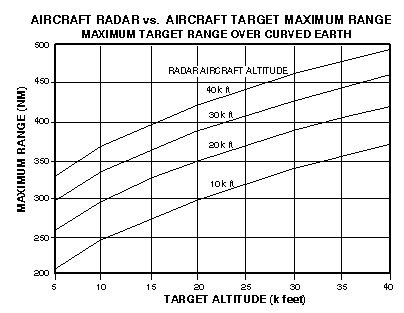

Figure 4 depicts the maximum range that a ship height antenna can detect a zero height object (i.e. rowboat etc).

In this case "H" = 0, and the general equation becomes:

Where h_r is the height of the radar in feet.

Figure 5 depicts the same for aircraft radars. It should be noted that most aircraft radars are limited in power output, and would not detect small or surface objects at the listed ranges.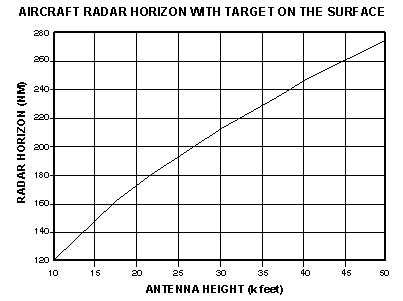

Other general rules of thumb are (with R in NM and aircraft altitude in feet):

For Visual SAR:

For ESM: